Fun with Virial Coefficients

We are still working on this. Some follows. Try later for more.

Now let's look at some behaviors of the variation of the second virial coefficient (B) with temperature. First we will look at an atom, He. We know that there will only be dispersion interactions which stabilize the pairs of helium atoms and it is a very small atom so we anticipate that the pairs will not be stable over a very large temperature range. The data plotted below is from the book "The Virial Coefficients of Pure Gases and Mixtures", edited by Dymond and Smith and published by thomson Litho Ltd, East Kilbride, Scotland.

BvsTHe

We were very good predictors weren't we? We see that B begins negative which means that (refer back to the section on contributions I-III) the pair interaction is negative which means that pairs of helium atoms are forming stable clusters at very low temperatures. We see very small negative values for B and we see that it crosses zero at about 22 K. Remembering that kT (k is Boltzmann's constant) is the energy equivalent of temperature on a molecular basis and RT (R is the ideal gas constant) is the energy equivalent on a mole basis, we can then calculate the approximate energy stabilization value for the He atom pair clusters. Using 22 K we get a value of .0437 kcal/mol for the pair stabilization energy which is very low as we would expect.

Now let's consider a molecule. Nitrogen is a rather simple molecule (from some perspectives) so let's see what B vs T looks like for it. The following plot contains two sets of data. The lower T set is from D. White, J.-H. Hu, and H. L. Johnston, J. Chem. Phys. 21 1149 (1953) and the upper T set (you can see the slight descrepancy appear at about 200 K) is from J. A. Huff and T. M. Reed, J. Chem. Engng. Data 8 (1963).

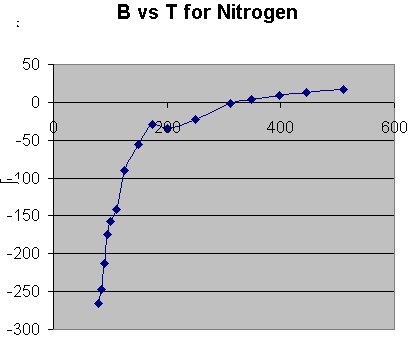
BvsTN2

We again see that initially B is negative which means that we do have stable pair clusters. We also note that the B values are considerably larger than for He. As the temperature increases we see that B becomes less negative until at about 348.2 K it becomes positive (+ 3.1) meaning that pair interactions are now repulsive (no stable pairs exist at this temperature and above it). we then see that RT at this temperature is .692 kcal/mole. B is -0.52 at 323.2 K and RT at this temperature is .642 where B is slightly negative. I do not have the data where B is exactly zero although we could obtain it from the above plot. From this information we see that the energy required to disrupt the stable pair nitrogen molecules is between .692 and .642 kcal/mole.

So now let us look at another molecule, CO₂ as shown below. This data is taken from S. Angus et al, International Thermodynamic Tables of the Fluid State Carbon dioxide, Pergamon Press, Oxford, 1976.

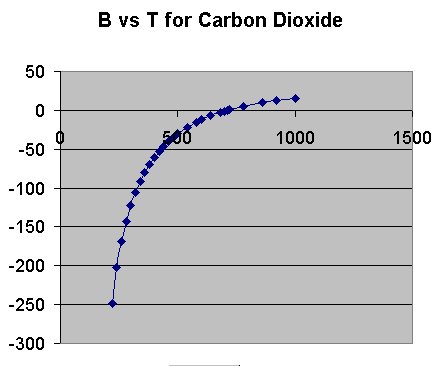
BvsTCO2

Here we see a somewhat different picture than for N₂. The second virial coefficient for CO₂stays negative over a larger temperature range than for N₂ meaning that pair clusters of carbon dioxide molecules are more stable than pairs of nitrogen molecules. That makes sense to us, doesn't it? Carbon dioxide does not have a permanent dipole moment, nor does it have hydrogen bonds; however it is a larger molecule with a larger polarizability and thus the intermolecular interactions due to dispersion forces will be larger for carbon dioxide than for nitrogen. The zero value for B occurs between 710 K and 720 K which would correspond to an energy range of 1.411 kcal/mol and 1.431 kcal/mol. So we see that the pair stabilization energy for carbon dioxide is roughly twice that for nitrogen molecule pairs.