II. Charge-Charge

A. Basics

This is the easiest interaction to study, but remember that for the case of ionic compounds there is no such thing as a molecule. We will then be dealing with ions in solution and we will choose the solvent to be water. This force is understood by using Coulomb's law which says that the force between two charges separated by a distance r_ij is given by

F_ij = q_i*q_j/r_ij² .........................(3)

where q_i and q_j are the charges of two interacting charges on two separate atoms such as between a Na⁺ ion and a Cl^- ion and r_ij is the distance between the two ions. If q_i and q_j have the same sign then the force is positive and the interaction is termed repulsive. If q_i and q_i have opposite signs then the force is negative and the interaction is termed attractive. Remember that these are intermolecular forces so that these two ions are like in solution rather than as the ions in a NaCl ionic solid. The more concentrated the solution, the smaller the average distance of separation of the ions. So F_ij is inversely proportional to the square of the concentration. If the interacting ions are Na⁺ and Cl^- then q₁ is +1 and q₂ is -1 so that a plot of F vs r would look like

Now take a few minutes to think about this curve. Use the following questions to help your direction of thought:

What type of curve is this?

Does the curve approach a limit as r goes to infinity?

Does the curve approach a limit as r goes to zero?

The rate at which the curve approaches its limit as a function of r is an important criteria to compare among the various forces and potential energies as we will see later. Since the more ions we have in solution the smaller will be the average distance separating the ions, we see that the distance between ions, r, is proportional to the concentration of ions in solution.

B. More

Now we know that we don't have just two of these ions in solution. We actually have a very large number of these ions. If we have one mole of each of the ions then we have 6.023 x 10²³ of each of the ions. This number, Avogadro's number(N_A), is essentially infinity for most mathematical purposes. We know that strictly speaking, to a mathematician this is not true. However for many practical purposes this is an excellent working statement. So how do we deal with all of the interactions of all of these ions? We could calculate the total force among all of the ions as a sum of all of the pair interactions:

where each f_ij is given by equation 1 above so that we would have

and the sum extends over all i and j ions in solution. We would then have (for the Na and Cl ions situation)

F_t = -1/r₁₂ - 1/r₁₃ - 1/r₁₄ - 1/r₁₅ --------

-1/r₂₁ - 1/r₂₂ - 1/r₂₃ - 1/r₂₄ --------

-1/r₃₁ - 1/r₃₂ - 1/r₃₃ - 1/r₃₄ --------

and continuing for all ij values

Note that some of the pair values are repeating: for every 1/r_ij we also have a 1/r_ji and we don't want to count the interactions twice. Therefore we will have to put 1/2 in front of the summation so that we can obtain the true summation of all pair interactions:

Chemists make use of a lot of series expansions so it is important to understand something about series convergence or divergence. Equation (6) seems obviously convergent since the various ion separations become larger as we move from some reference point in the solution toward the outer fringes of the solution. In the solid state (ionic crystal) the series converges to a value yielding what is called the Madelung constant. In the liquid state the convergence limit is not so easily determined because rather than a nice lattice arrangement of ions we now have a variable distribution function regarding the distance of ions from each other. We will not go into the use of such distribution functions at this point, but will just assume that the series expansion does converge so that we can use it. One would think that a series which diverged would be of no use for it does not approach a real limit. However, there are divergent series which are very important and they are called asymptotic series. The error function is an important function which falls in this category. We may get into the use of such series later.

C. More Again

Another important concept in intermolecular forces is the second virial coefficient which is given by

where V(r) is the pair interaction potential, R is the ideal gas constant, T is the temperature, and N_A is Avogadro's number. [An aside: whenever you see an RT or a kT , where k is Boltzmann's constant, you know that the units are in energy units. The difference is that RT says that the energy is on a mole basis and kT says that the energy is on a molecule basis. We will frequently use both measures.]

Why is the second virial expansion of considerable interest? It represents physically the relative stability of molecular pairs. And as pair interactions go, so goes the molecular system. Meaning what? Note that B₂ is a function of the temperature explicitly through T and implicitly through V(r) for as we will see later V is not only a function of r, but also of T for some types of interactions. If the second virial coefficient is never negative (meaning an overall attractive pair interaction), then the molecular system does not form any overall attractive situation and so is not stable. Are there any such real systems? Yes, remember that we are dealing with the liquid state and anything that normally sublimes rather than going through a liquid state would be such an animal.

Now since V(r) is the pair potential energy we need to transform our force into the potential energy. How do we do that? We have to remember a little physics. If the forces between the particles are only radially dependent, and if we define our zero potential energy of interaction to be the particles separated at infinity and at rest, then the work required to bring two particles from the distance r to the distance infinity is the same as the potential energy of interaction of the particles at the separation distance r. We know that the work is given by

and thus the potential energy would then be:

This is Coulomb's law expressed in terms of the potential energy rather than in terms of force. We can easily switch from one form to the other since, for radially dependent forces, we know that

f(r) = -dV(r)/dr ...........................(10)

So then the total V(r) for all pair interactions would be (similar to that above)

Can we then talk about a B₂ for ion interactions as the intermolecular forces? We have to look back at equation (7) and see about the convergence of the integral when V(r) is given by equation (11). What we actually see is that if the potential energy of interaction is only given by an ionic term like equation (11) then the integral of equation (7) diverges so we can not talk about a second virial coefficient for such a system.

But what about our comparison between methanol and water? Neither methanol nor water have any full ionic charges so how does the above apply to these molecules? Well, it doesn't if we don't have any ionic compounds in with them. However from our chemistry background we remember that oxygen has a higher electronegativity than carbon and hydrogen so that means that water and methanol will have partial charges on the atoms in the molecules. The reason for the partial charges is that, for example, in water since oxygen has a higher electronegativity than hydrogen the electrons will be more attracted to oxygen than to hydrogen and we will have the following partial charge distribution:

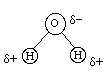
where delta+ is a partial positive charge and delta- is a partial negative charge. Since we now have a separation of charge -- the center of positive charge would be between the two hydrogen atoms and the center of negative charge would be on the oxygen atom - we see that the water molecule has a permanent dipole moment. We categorize molecules with permanent dipole moments as polar molecules. Similarly we see that methanol is also a polar molecule:

CH₃OH or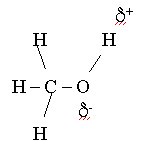

So we now have to consider dipole-dipole interactions. However before we go to that category of intermolecular forces, let us first examine the charge-dipole forces which are a little easier to examine.

III. Charge - Dipole

The situation is now a bit more complicated. A dipole consists of a negative charge separated from a positive charge by a distance l:

q⁺---_l----- q^-

So now we are considering the following situation:

Q⁺ -------- q⁺---------- q^-

The potential energy of interaction now depends upon R and before we do any summing over all angles (U(R,)), where R is the distance between the charge and the center of the dipole and is the angle between the charge and the line of the dipole. Before we do the summing over the angles, let's see what the potential of interaction would be if the angle were fixed so that we had the situation:

where is the angle that the dipole makes with the a - q⁺ line. The Coulombic potential of interaction is then just V₊₊ + V_+- where

V₊₊ = Q⁺q⁺/r₊₊ , where r₊₊ is the distance between q⁺ and q⁺ of the dipole

and

V_+- = Q⁺q^-/r_+- , where r_+- is the distance between q⁺ and q^- of the dipole.

But r₊₊ = R + �l cos(theta) and r_+- = R - �l cos(theta) (remember that l is the dipole distance), so

where x = l / R, and since we have taken the sign out of q there is not need to differentiate between q⁺ and q^- and there is no need to have the sign of Q signified so we have factored out q, Q, and R.

Now we can use a series expansion for the denominator expressions since we know that

1/(1 + x) = 1 - x + x² - .... and 1/(1 - x) = 1 + x + x² + .... (these expansions are used a lot in Chemistry)

so that we have

We have ended with this result by truncating the series expansions at the second term in each. We can do that because the dipole distance, l , is much less than the distance between the dipole and the charge,R, so that x << 1 and the terms raised to powers will be negligibly small.

But ql is μ, the dipole moment so that we finally have for the potential energy of interaction of a charge with a dipole oriented at angle :

However we are not yet through. Now we must remember that the dipole can be oriented in relation to the charge q⁺ in an infinite number of orientation angles. Let's look at a few different orientations:

Situation 1.) is a repulsive arrangement, situation 2.) and 3.) are both attractive arrangements. The dipole will be rotating about its center of gravity at some precession rate, but the attractive arrangements will be more energetically favorable than the repulsive arrangements. The more energetically favored arrangement will then be statistically favorable events. To account for the different statistical favoring of each arrangement, each arrangement must receive a weighting factor. The weighting factor is given by a Boltzman factor of

w = exp (-V/kT)...........................................(12)

where V is the potential of interaction between the charge and the dipole, k is the Boltzman constant, and T is the temperature in Kelvin. Again referring to the above three examples, we see that w₁ < w₃ < w₂. Why this order, you may ask. Remember that the potential energy of interaction is negative for an attractive arrangement and positive for a repulsive arrangement. Thus V₁ is positive and the same magnitude as V₂ which is negative. V₃ is negative but of smaller magnitude than V₁. Writing V to mean the absolute value of V (value without sign), we then have

w₁= exp(-V₁/kT), w₂= exp(V₂/kT), w₃ = exp(V₃/kT).........................(13)

where the sign of V has been considered within the (). Now it is easy to see (since abs(V₁₎=abs(V₂) >abs(V₂)) that w₁<w₃<w₂. Thus our Boltzman weighting factors are doing what they are supposed to do, give the more energetically favorable event the highest probability of occurrence. What we must do now is determine the average value of the interaction energy of the charge - dipole interaction by summing over all possible orientation angles with each angle having the appropriate Boltzman weighting factor. Since there are an infinite number of continuous possible angles of orientation, we will replace the summation with an integral. We will then have to evaluate

where we are assuming that the rotation occurs much faster than the variation in R so that we can assume R to be fixed during the rotation. The result is

V(r) = -Q²�²/(3kTr⁴)

We have changed from R to r to be consistent with all of our formulas where r is the distance between the interacting particles, but this distance is between the particle and the center of the dipole for this situation.

Here we see that the potential energy of interaction varies as 1/R⁴ whereas for the charge-charge interaction the variation was as 1/R. Then a plot of V(R) vs R for the two cases would look like

Hence we see that the charge-charge interaction decreases considerably slower with increasing R than the charge-dipole interaction. Remembering that R is directly proportional to concentration, we can then say that at any particular concentration the charge-dipole interaction will be less than the charge-charge interaction.

We still cannot talk about our methanol or water situations but we can talk about the Na⁺ and Cl^- interactions with the dipoles of methanol and water. Looking up the dipole moments of water and methanol we see that μ_water = 1.84 D (D stands for Debye, the standard unit of dipole moment) and that μ_methanol = 1.70 D. From our equation above we see then that the potential energy of interaction between say the Na⁺ ion and these molecules would be

V_water/Na⁺ = - 1.84²/(3kTR⁴) and V_methanol/Na⁺ = - 1.70²/(3kTR⁴)

where R is the distance between the charge and the center of the dipole. Then the ratio of the potential energies would be V_water/V_methanol = 1.17 so that there is about 17% more interaction of the sodium ion with the permanent dipole of water than with the permanent dipole of methanol. So what about the question of what happens to the boiling points of these molecules if we add some ions into the picture? We have seen that adding ions will then give us some ion-dipole interactions with the polar molecules. This attractive force will have the result of binding the water molecules in solution stronger than the methanol molecules so we would predict that the same amount of Na⁺ ions added to water and to methanol will raise the boiling point of both solutions over the boiling point of the pure solvents, but will raise the boiling point of water more than the boiling point of methanol will be raised. At this point you should do an experiment to determine if your theoretical prediction is correct. When you do you will see that indeed this is correct! Ain't science great?

So now let us add a discussion about another type of pair interaction so that we can more completely talk about our chosen molecular systems.

Web Author: Dr. Leon L. Combs
Copyright ©2012 by Dr. Leon L. Combs - ALL RIGHTS RESERVED