IV. Dipole-Dipole

Now we can explicitly look at the interactions between two water molecules, or between two methanol molecules, or between one water molecule and one methanol molecule. We now have a bit more complicated situation:

The procedure is exactly the same as the previous ion-dipole interaction, but we have to let both molecules rotate with weighting factors. The result is

V(r) = -2µ₁²µ₂²/(3kTr⁶)

where µ₁ and µ₂ are the dipole moments of the two polar molecules (could be water-water, methanol-methanol, or water-methanol.

Now we can try to predict which of the two molecules will have the higher boiling point. We look up the dipole moment of water and we find that it is 1.84 D (D stands for Debye, the unit for dipole moment) and for methanol we find the value 1.70 D. Using the above equation we would calculate the potential energies of interaction of the molecules to be

V_water/water = 2(1.84)⁴/(3kTr⁶) and V_{mthanol/mthanol} = 2(1.70)⁴/(3kTr⁶)

For fixed values of T and r, we then see that

V_water/water/V_{methanol/methanol} = 1.372

Now we know that the higher the intermolecular forces, the more energy is required for the molecules to become free into the gas state. The standard boiling point is the temperature at which the vapor pressure is equal to the standard atmospheric pressure. So the higher the intermolecular forces the higher the boiling point. If the boiling point were just directly proportional to the intermolecular forces, then we could predict the boiling point of methanol since we know that the boiling point of water is 100⁰C and since we have the ratio of the intermolecular forces above. Using that ratio, we then predict the boiling point of methanol to be 100/1.372 or 72.9⁰C. Looking up the experimental value we see that the boiling point of methanol is 64.7⁰C. Not such a bad prediction for a country boy! We have not only predicted qualitatively that the boiling point of water is greater than the boiling point of methanol, we have made a quantitative prediction which is about 12% in error. This is not a publishable result, for 12% error is considerable, but it is still meritorious.

But we aren't finished yet.

V. Charge-Induced Dipole

Another possible interaction involves an ion inducing a dipole moment in something else. An ion may induce a dipole in a neutral atom or non-polar molecule or it may induce a stronger dipole in a polar molecule and then the permanent dipole and the induced dipole can interact. What do we mean by "induce"? We know what I mean when I say that I could be induced to eat a chocolate bar, don't we? It means that the situation could be right that I could be caused to eat a chocolate bar even though I don't need one. Here I sit fairly comfortably since I just finished a peanut butter sandwich. But then you come along and offer me a chocolate bar. I just might then take it. Similarly for a non-polar molecule like carbon tetrachloride (CCl₄). It is very happy not having a permanent dipole moment but if an ion (like Na⁺) comes close by it, then the electron distribution of the non-polar molecule will be perturbed because of the close proximity of the positive charge of the sodium ion, and then the non-polar molecule will have an instantaneous dipole moment. Once the instantaneous dipole moment exists it can be stabilized by an interaction with the ion and we have a charge-induced dipole interaction. The situation is a bit difficult mathematically, but we end up with the formula

where is the polarizability. The polarizability is the ease with which the electron distribution can be perturbed from its original orientation/distribution and has units of volume (cm³ or ų - one Angstrom is 10^-8cm which is a common unit in chemistry and physics). From our high school chemistry we know that the polarizability increases as one goes down the periodic table of the species being polarized by the charge q. Polarizability values are not as easy to find as dipole moment values, but some values are the following:

Molecule or Atom	,Polarizability(Å3/molecule)	Tb(K)	Dipole Moment(D)
He	0.20	4.216	0
Ne	0.39	27.3	0
Ar	1.62	87.3	0
Kr	2.46	119.9	0
H2O	1.48	373.15	1.85
H2S	3.64	212.82	1.10
CCl4	10.5	349.85	0
C6H6	25.1	353.25	0
CH3OH	3.0	338	1.71
CH3F	3.84	195	1.81
CHCl3	8.50	334.85	1.01

From these values for water and methanol we can calculate the potential energies of interaction between the sodium ion and the induced dipole moment as the following:

V_water = 1.48/(2*r⁴) and V_methanol = 3.0/(2*r⁴)

The ratio is then V_water/V_methanol = .4933 so that there is about twice as much potential energy of interaction between the sodium ion and the induced dipole moment of the methanol molecule as there is between the sodium ion and the water molecule. Remember that there was about 17% more interaction of the sodium ion with the permanent dipole moment of the water molecule than with the methanol molecule. The reason is due to the sizes of the molecules water and methanol. Methanol is a larger molecule than water and its electron distribution is more easily distorted. Thus the sodium ion induces a larger dipole moment in methanol than in water. It can be shown that, for a sphere, the polarizability is equal to the cube of the radius of the sphere. Then assuming water and methanol to be spheres (which they are not), the differences in polarizabilities would be that the radius of the water sphere would be (1.48 = r³) 1.139 Å and the radius of the methanol sphere would be (3.0 = r³) 1.44 Å. This crude calculation shows the radius of the methanol "sphere" is about 26% larger than the radius of the water "sphere". Since the polarizability is proportional to the size of the molecule and is equal to the cube of its effective radius, as the size increases the ion-dipole interaction increases considerably.

VI. Dipole-Induced Dipole

Similarly to the above, a permanent dipole may induce a dipole in a neutral atom or non-polar molecule or it may induce a stronger dipole in a polar molecule and then the permanent dipole and the induced dipole can interact. Again our non-polar molecule like carbon tetrachloride (CCl₄). is very happy not having a permanent dipole moment, but if a polar molecule (like CHCl₃) comes close by it, then the electron distribution of the non-polar molecule will be perturbed because of the partial charges on the polar molecule and then the non-polar molecule will have an instantaneous dipole moment. Once the instantaneous dipole moment exists it can be stabilized by an interaction with the polar molecule and we have a dipole-induced dipole interaction.

This situation is again rather complicated to deal with mathematically, but the result is that the potential energy of this interaction is

where is the polarizability of the molecule being polarized and μ is the dipole moment of the molecule with the permanent dipole moment.

For our two applications we see that

V_water/water = 1.84²*1.48/r⁶ and V_{methanol/methanol} = 1.70²*3.0/r⁶

which gives a ratio of V_water/water/V_{methanol/methanol} = .5779 which says that the water-water interaction is less than the methanol-methanol interaction. But the dipole-dipole interaction showed the opposite trend with a ratio of 1.372 which would indicate that when we combine these two contributions we would be saying that the boiling points of both should be about the same, and we know that such is not true. So we still have some work to do.

What we have so far for these molecules (no ionic charges) is

Note that for the inert gases, as the polarizability increases the boiling point similarly increases as we might expect from the above discussions for they have no permanent dipole moment and no charges - wait a minute, no permanent dipole moment! So from whence cometh the attractive interactions? You guessed it - we have another contribution to consider.

VII. Induced Dipole-Induced Dipole (or Dispersion, or London Dispersion) Interaction

The first name tells us exactly what this interaction is. This type of interaction exists between any molecular or atomic species and thus is very important. Once an induced dipole exists in some species then that induced dipole can induce a dipole in another species and then we have an induced dipole - induced dipole interaction. A derivation of the potential energy of interaction is rather complicated and one can actually find a couple of different forms of the equation. The derivation is based upon quantum mechanical concepts and is beyond the scope of this module. One useful form of the energy is given by

where I is the first ionization potential for each species and is the polarizability of each species. Another form of the equation applicable to molecules is

where h is Planck's constant and ₀ is the fundamental vibrational frequency of the molecule (there is no vibrational mode for an atom, of course). The term ₀ is related to the energy of the first vibrational energy mode of the molecule and there is not a lot of variation in this value among molecules, at least not to the extent that there is variation in the polarizabilty. Thus most of the variation among molecules in the dispersion interaction arises from the polarizability differences.

Comparing our two molecules again, we see that

V_water/water is proportional to 1.48² and
V_{methanol/methanol} is proportional to 3.0²

and we then have a water/methanol ratio of .2433 which is now telling us that the methanol boiling point should be considerably above the water boiling point and we know that such is not correct. What is the problem? Yep, you guessed it, we have another attractive term to consider which we did not list on our original list of 7.

VIII. Hydrogen Bond

This type of attractive interaction is an electrostatic attraction between two strong and specifically oriented dipoles at least one of which contains a hydrogen atom. We did not include it earlier as a dipole-dipole interaction because in the earlier discussion it was assumed that the dipoles rotate and that the dipole length was much less than the distance of interaction and neither of these assumptions are valid in this situation. Remember that we are discussing intermolecular forces and potentials so when we talk of a hydrogen bond in this context we do not mean the bond between the oxygen atom and one of the hydrogen atoms in the water molecule. We are talking about an attractive force between a hydrogen in one molecule and a negative portion of the dipole in another molecule. The hydrogen must be bonded by an intramolecular force to a very electronegative atom (O, F, Cl, and N to a lesser extent) so that the hydrogen atom will have a large positive partial charge (sometimes close to one). Let's look at some examples. First look at hydrogen fluoride:

This is the strongest hydrogen bond because F is the most electronegative atom in the periodic table so that the hydrogen atom has the largest partial charge of any such chemical bond. You can easily see that HF can be held by hydrogen bonds as dimers, trimers, etc. In fact the bond is so strong between the molecules that HF monomers do not even exist in the gas phase.

Now look at acetic acid where we see two hydrogen bonds holding the pair of molecules together:

Now let's look at the water molecules as they interact:

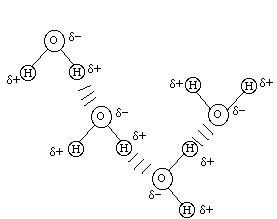
For water we can see several possibilities for multiple hydrogen bonds stabilizing the pair of molecules. For methanol we can only see one possibility for hydrogen bonding

The oxygen does not have as much partial negative charge in methanol as it does in water because the C atom draws away some of the negative charge. Therefore the hydrogen atom in methanol does not have as much positive charge as in water. The result is that the hydrogen bond in methanol is not as strong as it is in water. It is the hydrogen bond effect which explains why the boiling point of water is greater than that of methanol.

No radial dependence can be written for the hydrogen bond interaction but they are very strong forces and must always be considered if they exist in the system under consideration.

IX. Van der Waals Repulsion

This is the final force or potential to consider and is the only repulsive force. This repulsive force is quantum mechanical in nature and a specific formula for it cannot be written which would be specific for all cases. All we can denote is the radial dependency with a proportionality factor C:

V(r) = C/r¹²

This is a very short range force, but one which is dominant at small separations. Now we see the form of the equations which make up the curves in Figure 1:

V⁺ = C/r¹²

+ hydrogen bond interaction if it exists

We usually don't have full-fledged ions to consider in the interactions, in which case we see that we generally have an equation of the form (putting q = 0)

V = C/r¹² - A/r⁶

This type of interaction potential is said to be a Lennard-Jones "6-12" type potential. One actual fomr of the Lennard-Jones "6-12" potential is given by:

where is the distance at which V(r) = 0 and is the minimum of the potential energy well (see Figure 1a). It is easy to show that the minimum energy, V(r) = -, occurs at the distance r = 2^1/6.

The Lennard-Jones "6-12" potential works reasonably well for small non-polar molecules.

Returning to our derivation, we see that our equation for A would be

Remember that C does not have a general form, because it must be determined by quantum mechanical calculations. Also remember that there is no general term for the hydrogen bond energy, but we must always consider it if such exists.

Now let's look at some fun applications of what we have learned. If you are ready now go to the next page

Web Author: Dr. Leon L. Combs
Copyright ©2012 by Dr. Leon L. Combs - ALL RIGHTS RESERVED