Section Three

Chapter Eight, Section Three

OBJECTIVES

Understand the concept of a buffer and how it functions.
Understand titration.
Understand the concepts of equivalents and normality.

I. Buffers

If the pH of blood varies much away from the range of 7.35 to 7.45, the person will cease to biologically function. Anything lower than 7.35 is called acidosis and anything higher than 7.45 is called alkalosis. We ingest things with a high pH (colas, oranges, tomatoe joice, etc), so how does the body maintain the pH of blood in a range in which the person can live? We have a wonderful buffer system that allows us to continue to function even when we abuse our digestive system considerably. A buffer solution is one whose pH does not change very much when H₃O⁺ or OH^- ions are added to it.

A buffer is made by adding equal quantities of a weak acid and its conjugate base. For example, we could add 1 mole of acetic acid (a weak acid, CH₃COOH) and 1 mole of sodium acetate (the conjugate base is the acetate ion, which will be formed when sodium acetate is added to water) to water and we would have a buffer solution. Now if H₃O⁺ is added to the buffer solution, we have a lot of acetate ions (CH₃COO^- to neutralize it. If OH^- ions are added we have a lot of acetic acid to neutralize it. Thus a buffer functions by having enough of the appropriate ions in solution to neutralize any added H₃O⁺ or OH^- ions.

It turns out that it is rather easy to determine the pH of a buffer solution. If we make a buffer by mixing equimolar amounts of any weak acid and its conjugate base then the pH of the buffer solution is just the pK_a of the acid.

pKa

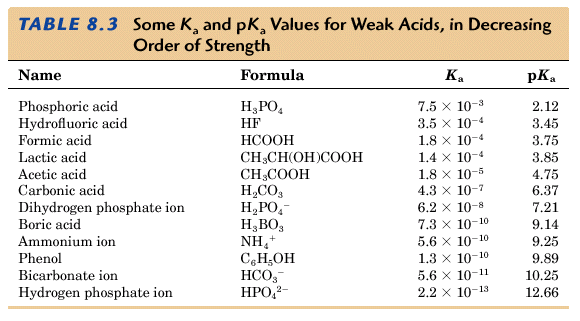
From the above table you can see that we can prepare a buffer solution which will maintain a pH over a very broad range of pH's. If we want to maintain the pH at about 9.9 we could use phenol and a salt of phenol in equal molar amounts.

The buffer capacity of a buffer is the extent to which a buffer can prevent a significant change in pH upon the addition of an acid or a base. The buffer capacity obviously depends upon the molar concentration of the components of the buffer. A buffer made using 1 molar concentration of a weak acid and its salt will have 10 times the buffer capacity of a buffer made using 0.1 molar concentration of acid and its salt.

The blood buffering system is truly amazing. The average pH of blood must be maintained at 7.4 within 0.1 pH unit. Any change in pH greater than 0.1 pH unit is pathological. The body uses three buffer systems: carbonate, phosphate, and proteins (discussed in the second semester of the course).

The carbonate buffer solution is made up of 0.025 molar concentration HCO₃^- and 0.0025 molar concentration H₂CO₃. The 10 to 1 ratio is required because if we used equimolar amounts the pH would be maintained at about 6.37 (see pK values above). This system is more effective at buffering added acids than added bases.

The phosphate buffer solution is made of a 1.6 to 1 ratio of HPO₄^2- and H₂PO₄^- to maintain a pH of 7.4. If these two buffer solutions were not made up exactly in this way, we could not exist. Rather phenomenal!

II. Titrations, Equivalents, and Normality

Titration is an experiment in which one reactant completely uses up another reactant in a quantitative manner (meaning that we know exactly how much of each reactant was present when the reaction was completed. For an acid-base titration we use a buret to add a known amount of an acid or base to a known amount of base or acid. The point at which the reaction is complete will be neutralization for the acid-base case and can be determined by watching for an appropriate color change using an indicator. We talk about a titration being complete when one equivalent of one reactant has exactly used up one equivalent of the other reactant. For an acid-base reaction, the equivalent weight is defined as the formula weight divided by the number of H⁺ or OH^- ions produced in solution. Thus the equivalent weight of HCl is just the formula weight divided by one. The equivalent weight of H₂SO₄ is the formula weight divided by two. The equivalent weight of NaOH is just the formula weight, but the equivalent weight of Ba(OH)₂ is the formula weight divided by two.

The normality of a solution is the number of equivalents (rather than the number of moles) of a substance per liter of solution. Normality is always equal to or greater than the molarity. At the end point of the titration, Eq_acid = Eq_base and the number of equivalents is just the normality multiplied by the volume of the solution (in the same way that the number of moles is the molarity multiplied by the volume of the solution). We then have that

V_acidN_acid = V_baseN_base

With this relationship we can now answer questions such as "If 50.00 mL of an acid solution is titrated with 0.152 N base, and it takes 27.5 mL of base to reach the end point, what is the normality of the acid?

ASSIGNMENTS

Here is a high school site for buffers buffer site.
This site contains information on buffers, titrations, and other concepts that can be useful to you.

QUIZ ONE

After you have studied this material and practiced some problems, take quiz three. If you score at least 80 on the test then you are ready to continue to the next section.