| Chapter Five, Section Two |
I. Avogadro's Law and the Ideal Gas Law
In 1811 Avogadro developed the hypothesis:
Avogadro's hypothesis was proven 50 years later by Cannizzaro and then people accepted it and considerable progress in understanding the molecular world began. Avogadro's hypothesis led people to determine that at STP 22.4 liters of any gas will weigh the gram molecular weight of the gas: 22.4 liters of H2 will weigh 2 grams, 22.4 liters of O2 will weigh 32.00 grams, etc. You see that Avogadro's hypothesis led the scientists to understand that the volume of a gas is proportional to the number of moles of the gas.
So now we have:
If we combine all of these we will have
V = constant*(nT/P) and if we let the constant be R then we have
V = nRT/P or PV = nRT ....... the ideal gas equation of state.
The value of R depends upon the units:
R = PV/(nT)
R = 0.082056 latm/molK = 82.056 cm3atm/molK
R= 1.987 cal/molK
R = 8.3144 J/molK
So what value we use for R will depend upon the problem that we are working.
So we have an equation of state (EOS): PV=nRT. You note that I called this the ideal gas equation of state. Why did I call it the ideal gas equation of state?
Good question. Solve for V and we get
V = nRT/P
Now what happens to V as P goes to infinity or as T goes to zero? The volume goes to zero right? So what happened to our gas? It disappeared as the pressure increased towards infinity!! This means that the gas does not have any size!! Clearly this is not for a real gas. Thus we call our equation of state an ideal gas equation of state(IG EOS). We will explore this further later.
II. Dalton's Law and Graham's Law
What if we have a mixture of gases rather than just one gas? Dalton discovered that the pressure is equal to the sum of the partial pressures of the gases in the mixture. The partial pressure is the pressure that the gas would exert if it were alone in the same container in which the mixture is present. The partial pressure of the ith gas is then
Pi = niRT/V and the total pressure by Dalton's law is
P = SUM Pi = P1 + P2 + P3 + ...
or
P = SUM niRT/V = RT/V SUM ni = (RT/V)ntotal
We can get a relationship between the total pressure and the partial pressures quite easily. Look at the ratio of the partial pressure to the total pressure:
Pi/Ptotal = (niRT/V)/(ntotalRT/V) = ni/ntotal = Xi .. the mole fraction of the ith gas. Therefore we have
Pi = XiPtotal
Let's work an application of what we have learned so far with Dalton's law and the relationship between partial pressures and total pressure. What is the total pressure of a mixture of 1.0 g of hydrogen gas and 5.0 g of helium gas confined to a vessel of volume 5.0 liters at 20 0? Also what are the partial pressures of each gas?
We know that P = ntotalRT/V so we need the total number of moles of the gases in the mixture.
ntotal = 1.0 g H2*(1 molH2/2.0 g H2) + 5.0 g He*(1 mol He/4.0 g He) = 0.5 moles H2 + 1.25 moles He = 1.75 moles
So the pressure is
P = ntotalRT/V = 1.75 moles*(0.082 latm/molK)293K/5.0 l
P = 8.4 atm
Now how about the partial pressures? From the moles of the individual gases, we can calculate the mole fraction of the gases:
Xhydrogen = 0.5/1.75 = 0.29
Xhelium = 0.71
Therefore
Phydrogen = 0.29 * 8.4 atm = 2.4 atm
Phelium = 0.71 * 8.4 atm = 6.0 atm
Check to see that the sum of the partial pressures is the total pressure and we see that 2.4 + 6.0 = 8.4.
We can also develop now a useful equation that will help in dealing with some situations. From the ideal gas EOS we can solve for R and get
R = PV/nT
Now since this is a constant it has the same value for one set of state variables as it does for another set of state variables. That means that
R = P1V1/n1T1
= P2V2/n2T2
This equation would be useful for solving problems where there are two sets of conditions which are somewhat different and on variable is unknown. For example, what is the volume of a baloon at temperature 500 K and pressure .750 atm when you know that the volume of the baloon at temperature 300 K and pressure 1.00 atm is 2 liters (n will be the same for we don't change the contents of the baloon. Give that problem a try. The answer is 4.44 liters.
One further extension of the IG EOS is helpful which just involves a little rearrangement and the definition of density and moles. So
PV = nRT = (wt/MW)RT where we used the definition of mole. Now divide both sides by V:
P = (wt/V)RT/MW and recognize that weight over volume is density, D:
P = DRT/MW so now you can use density data in the IG EOS.
III. Intermolecular Forces
The prefix "inter" means between or among. Intermolecular forces then are the molecular forces between different molecules (like between two different water molecules). The following table lists the types of intermolecular forces that we will consider. It also lists the relative strengths of these attractive forces. It is important to note that these are all attractive intermolecular forces.
| Type of Intermolecular Attraction | Relative Strength |
| London disperson forces (every molecule has these) | Weakest |
| Dipole-dipole attractions (exists between polar molecules) | Intermediate |
| Hydrogen bonding (attraction between -OH, -NH or FH on one molecule and any O, N, or F atom in another molecule) | strongest |
Dispersion forces increase as the size of the molecule increases. Thus the dispersion forces between different CH3CH2CH2CH2CH3 molecules would be larger than that between different CH3CH2CH3 molecules.
Of course, to have dipole-dipole attractions the molecule must have a permanent dipole moment. Molecules such as water do indeed have a dipole moment so there would be dipole-dipole attractions between different water molecules and other polar molecules.
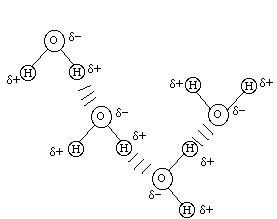
Hydrogen bonding is very important for it exists in many biochemically important molecules. It is a very strong force between different water molecules as noted below:

Be sure that you understand the hydrogen bond intermolecular force and are able to predict which molecules would exhibit such an interaction.
IV. Liquids
Liquid molecules have a closer nearest-neighbor distance of separation than gases and thus exhibit very different properties than liquids. They don't fill all available space, rather they tend to "glomp" together. Therefore the density of liquids is much greater than that of gases. It is also very difficult to compress liquids. The molecules do move around a lot so that the liquid state does not have a characteristic shape as the solid state does.
The molecules in the center of a liquid have different forces on them than the molecules at the surface. The center molecules are completely surrounded by other molecules so that the forces of interaction are balanced. However the surface molecules only have vapor molecules above them and they don't interact as strongly with them as they do with the liquid molecules. Therefore there is a resultant force on the surface of the liquid which tends to stabilize it. This force is called surface tension and is the reason that some small insects can walk on the surface of water.

After you have studied this material and practiced some problems, take quiz two. If you score at least 80 on the test then you are ready to continue to the next section.

Web Author: Dr. Leon L. Combs
Copyright ©2001 by Dr. Leon L. Combs - ALL RIGHTS RESERVED