





















| E4 | n=4;l=0,1,2,3 | 4s,4p,4d,4f |
| E3 | n=3;l=0,1,2 | 3s,3p,3d |
| E2 | n=2;l=0,1 | 2s,2p |
| E1 | n=1;l=0 | 1s |
In the last column you see that all of the "orbitals" with the same n value have the same energy. In quantum mechanics this phenomena is called degeneracy. So we say that the 4s, 4p, 4d, and 4f are energy degenerate meaning that they all have the same energy. We saw in our last discussion that the energy only depended upon the n value. This is true for hydrogen, but as soon as a second electron is added, like for the helium atom, the degeneracy is removed and the "orbitals" with the same n values no longer have the same energy.
When we try to solve the SE for helium or for any system with more than one electron we encounter a mathematical problem that nobody has been able to solve exactly (analytically). However the approximation techniques have become very sophisticated and we can solve the SE for very large molecules with great accuracy now.
When we have a system with two or more electrons the energy is now a function of n and l. So we then use the "n + l" rule to determine which combination of n and l have the lowest energy: "The combination with the lowest value of n + l has the lower energy. If two combinations have the same value of n + l then the combination with the lower n value has the lower energy."
Then using the above n + l rule we can develop the following ordering of energy levels, starting with the lowest energy and proceeding to higher energies:
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d <5p < 6s < 4f < 5d < 6p < 7s < 5f < 6d < 7p
To check this out, below I have written the n + l value for each n and l value above. Make sure that you understand this.
1< 2< 3 = 3 <4 = 4 <5 = 5 = 5 <6 = 6 = 6 < 7 = 7 = 7 = 7 < 8 = 8 = 8
You see that whenever the n + l value was equal, I choose the pair with the lower n value first. For example, 3p goes before 4s. If you grasp this rule you can use this as a basis to easily write the quantum numbers for any electron in the periodic table. We do have to know a couple of more concepts that we need for such a task:
The Pauli Exclusion Principle which says that no two electrons in the same atom can have all four quantum numbers the same.
The Hund Rule which says that when you are adding electrons to build up an atom the electrons prefer to maintain the same spin (either spin up or spin down) as long as possible.
We will now demonstrate the application of the above three rules to build up the periodic table.
We always start with the lowest possible energy which is the 1s level. So hydrogen will have the electron configuration:
1s ---- n = 1, l = 0, ml = 0, ms = -1/2;
We will always assume that the spin down (ms = -1/2;) quantum number is the one with the lowest energy.
We can form the electron configuration for helium by adding an electron with spin up :
1s2 ---- n = 1, l = 0, ml = 0, ms = +1/2
We used the n + l rule and the Pauli exclusion principle which allowed us to add another electron with the n, l, and ml values because we could make the ms value different.
Now we go to lithium and we can't use the 1s level anymore without violating the Pauli exclusion principle. So the third electron we add will be a 2s electron.
So we have the electron configurations for the first three elements:
H 1s
He 1s2
Li 1s22s
As we added another 1s electron to the hydrogen electron configuration to get the helium electron configuration, we can add another electron to the helium electron configuration to get the beryllium electron configuration;
Be 1s22s2
What are the four quantum numbers for the last electron added to form the beryllium electron configuration? Answer is at the bottom of this page.
Now we are ready for boron. We are through with the 1s and 2s levels without violating the Pauli exclusion principle so we now go to the 2p level:
B 1s22s22p
Now with the 2p level we have three ml values to work with (-1, 0, 1). Again we will start with the negative value for the lowest energy so that the four quantum numbers for the last electron added to boron are
n = 2, l = 1, ml = -1, ms = -1/2
When we go to carbon we can either go to ml = 0 and keep the ms = -1/2 or we can keep ml = -1 and change ms to +1/2. Which should we do? Remember Hund's rule? Yup. So we keep the ms = -1/2 and change ml to 0. Carbon will then have the electron configuration
C 1s22s22p2
and the last electron added has the four quantum numbers
n = 2, l = 1, ml = 0, ms = -1/2
Now we go to nitrogen and we can still keep ms = -1/2 by changing ml to +1. So nitrogen will have the electron configuration
N 1s22s22p3
and the last electron added has the four quantum numbers
n = 2, l = 1, ml = 1, ms = -1/2
Now to determine the electron configuration for oxygen we must change ms to +1/2 and start the variation of ml over again starting with -1. Then the electron configuration for oxygen will be
O 1s22s22p4
and the last electron added has the four quantum numbers
n = 2, l = 1, ml = -1, ms = +1/2
Then for fluorine we can continue the variation of ml so that we have
F 1s22s22p5
and the last electron added has the four quantum numbers
n = 2, l = 1, ml = 0, ms = +1/2
Similarly for neon we will have
Ne 1s22s22p6
and the last electron added has the four quantum numbers
n = 2, l = 1, ml = +1, ms = +1/2
Now we are through with 1s, 2s, and 2p. Make sure that you understand this.
If I use \ for spin down and / for spin up, I can make the following table to further illustrate what we have done above.
| Element | Electron Configuration | 1s | 2s | 2p |
| H | 1s | - | - | |
| He | 1s2 |  | - | - |
| Li | 1s22s |  | 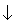 | - |
| Be | 1s22s2 |  |  | - |
| B | 1s22s22p |  |  | 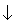 |
| C | 1s22s22p2 |  |  | 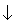 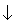 |
| N | 1s22s22p3 |  |  | 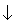 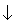 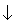 |
| O | 1s22s22p4 |  |  |  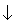 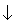 |
| F | 1s22s22p5 |  |  |   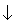 |
| Ne | 1s22s22p6 |  |  |    |
You can see how the electron spins are kept the same as long as possible and then we start pairing them (matching a down spin with an up spin) We follow all three rules and can build up the periodic table.
A shorthand is also possible to use as we progress throughout the periodic table. As long as you understand what you have done, it is redundant to keep repeating the electron configuration of each row. For example, we can write
Li as 1s22s or we can write it as [He]2s,
where we have written [He] for its electron configuration. Similarly we can write
Na as 2s22s22p63s or we can write it as [Ne]3s.
This shorthand will save some effort, but you must know what [Ne] stands for in electron configuration notation.
Practice, practice, practice.
Question: How many unpaired electrons does P have? Email your answer to me, with an explanation.
 Here is a good site for an overview of quantum numbers and electron configuration.
Here is a good site for an overview of quantum numbers and electron configuration.
 Here is a site which explains the building of the periodic table using the quantum numbers.
Here is a site which explains the building of the periodic table using the quantum numbers.
Answer: n = 2, l = 0, ml = 0, ms = +1/2.
| Now take a practice quiz to help you understand if you understand the basic concepts. |
| You must use your real name when it asks for a name. |
| The test will only submit when you have answers all of the questions correctly. |
| If you are not taking this course for credit please do not answer all the questions correctly for I don't want to be flooded with email answers to the tests. |

Web Author: Dr. Leon L. Combs
Copyright ©2001 by Dr. Leon L. Combs - ALL RIGHTS RESERVED