Quantum Mechanics

The next model was developed simultaneously by Schroedinger and Heisenberg, but since Schroedinger's model was more easily understood by most people at the time it was the model that received the most credit. Schroedinger developed his famous equation in 1925:

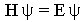
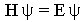
Where H is the Hamiltonian operator for the molecular or atomic system which contains mathematical terms for the kinetic and potential energy, E is the total energy of the system, and 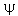is the wave function for the system. This wave function contains all of the information about the system and mathematical methods of extracting the information were quickly developed

One of the most important developments in helping to understand applications of the SE was Heisenberg's uncertainty principle developed in 1927:

HUP

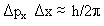
The HUP contains a P_x and a X where the now does not mean final "minus initial" as previously, but it means the uncertainty in the value of x and the uncertainty in the value of p_x where p_x is the momentum in the x direction (m * v_x where v_x is the x-component of velocity) and x is the x-coordinate of the system. When the uncertainty in the value of something goes to zero that means that we know exactly what that value is. So if we know exactly what the x-coordinate of the particle is then X is zero. Solve the above HUP for P_x and you will see that X is in the denominator on the right hand side of the equation and if X is zero what is P_x? Problem, right? If the uncertainty in the x-component of momentum is infinity then we have absolutely no knowledge of the value of that variable! So if we know exactly where the particle is then we have no idea of the value of the momentum of the particle -- it's allowable values range over all space! And since momentum is related to energy (check it out) then if we know exactly where the particle is we have no idea of what it's energy is! Similarly if we know exactly what it's energy is then we have no idea of where it is! Strange but true

The HUP means that we can only talk about regions of possible existence of electrons about an atom or molecule. We cannot have orbits because the definition of an orbit requires that we know energy and position simultaneously. We do call 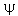the "orbital" but the definition of an "orbital" is that it is a one-electron wave function.

We can solve the SE for a hydrogen atom and we get the same energy expression as obtained by Bohr for his atom model. This means that the energy differences will give the same value for the Rydberg constant as obtained by the Bohr model which is required. However we get much more information with the SE because of the wave function from which we can obtain all information about the hydrogen atom including information about why atoms combine to form molecules.

help Go here for an illustration of a comparison of the Bohr atom and the Schroedinger equation.

Solving the SE is beyond the scope of this book (this is reserved for physical chemistry and modern physics). However let me say that when we solve the SE for the hydrogen atom we get mathematical series for solutions. A mathematical series is of "no" use unless it converges to distinct values. If the series does not converge it is called a divergent series. The requirement that these series solutions of the SE for hydrogen converge results in the three quantum numbers and the relationships among them:

n = 1,2,3,4,....
l = 0,... n-1
m_l = -l,-l+1,-l+2 ... 0, 1, 2, ..l

Before I comment further on these quantum numbers, let's talk a bit about the wave function. The wave function will be a function of these three quantum numbers so we would designate it with subscripts n, l, m_l. The wavefunction itself is an imaginary function. Here imaginary does not mean that it does not exist but is a mathematical term meaning that the function contains i which is the square root of -1, and thus it is not possible to visualize the function. However we can visualize the function times it's complex conjugate (same function with -i wherever i appears in the original function). This is indicated as below

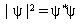sighsquared .......eq 1

Where the * means the complex conjugate of 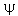. Now I know that this is much more than you want to know at this time, but I want you to have some idea of where this stuff comes from rather than just think that it is magic.

Equation 1 is very important. It affords us a method of determining the most probable location of the electron -- remember that the HUP says that we cannot know energy and position exactly. From this equation we can get two different types of probability distributions of the electron about a nucleus. We can determine the angular probability density or the radial probability density. Probability density means exactly what it says; it is a density map of angular or radial dependence of the electron from the nucleus. Here is a site where you can see the angular probability density map and you can vary parameters.

The density of dots represents the amount of charge of the electron at that location. so the region with the highest density of dots represents a place with a large fraction of the charge of the electron and hence a more likely place to find the electron. Remember that we have no way of knowing how the electron traverses about the nucleus. The best we can do is plot these diagrams which show us the most likely places to find the electron when it is described by particular combinations of the quantum numbers. What the type of density maps show are regions where we have a 95-99% probability of finding that particular electron.

The other type of probability density diagram is a radial probability diagram where we look at the probability of finding the electron at particular distances from the nucleus regardless of the angular probability. You can see some of these diagrams in your text.

Now I know that I am fighting a losing battle, but it is incorrect to talk about these probability diagrams as pictures of orbitals. However this terminology is widespread in all freshman chemistry books and even in most physical chemistry books. So I will use the terminology also even though it makes me cringe. In this terminology they talk about the "size of an orbital" which really means the outer diameter (95-99% region) of a probability density diagram.

Now let's return to a discussion of the quantum numbers. So in this parlance, n is called the principal quantum number and is related to the size of the orbital ":(". The larger the n value the "larger the orbital".

We can see the energy dependence by looking at the one-electron atom the energy which is given by

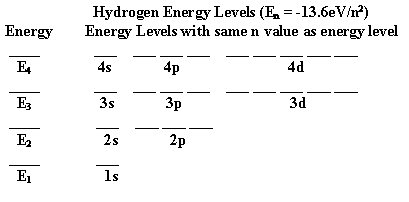
Ehydrogen

We see that as n increases the energy becomes less negative by the square of the n value (remember n varies as 1,2,3,4,....). The most negative value we could call E₁ and then we would have

E_n = E₁/n² , n = 1,2,3,4,... and remembering that E₁ is negative. The E₁ for hydrogen is -13.6 eV (electron volts, where one electron volt is 1.602 x 10^-19 joules). Then for hydrogen we have

E_n = -13.6 eV/n², n = 1,2,3,4,...

The l quantum number is called the angular momentum quantum number and it is related to the "shape of the atomic orbitals". We represent values of the l quantum numbers by the following letters:

value of l 0 1 2 3 4

letter used s p d f g

These letters originate from the atomic spectroscopy terms sharp (s), principle (p), diffuse (d), and fine (f). After f we just follow the alphabet without repeading any letters.

We use the notation of writing "nl" for the value of the n and l quantum numbers using the above letters for the l values. Thus a 1s orbital would be an orbital described by the quantum numbers n = 1 and l = 0. A 2p orbital would be an orbital described by the quantum numbers n = 2 and l = 1. Question: Is a 1p orbital possible? Answer is at the bottom of the page. Similarly for other combinations of n and l values.

The remaining quantum number, m_l is called the magnetic quantum number and is related to the orientation of the orbital in space

There is another quantum number which does not originate from the solution of the SE. It is the m_s quantum number and has the values +1/2 or -1/2. It is the spin quantum number. Now since we can't see an electron, we don't know what it is really doing (or it's path), but this quantum number expresses the fact that the electron has an associated magnetic field in either the up direction or the down direction (relative to it's coordinate system). A classical charged particle which is spinning would generate such a magnetic field, but since the electron is not a classical particle, we don't know what it is doing. However we do refer to this as the spin quantum number.

help This site will give you an illustration of various quantum mechanical orbitals.

Answer: No. A 1p orbital would have n = 1 and l = 1, but l can't be equal to the n value

Now take a practice quiz to help you understand if you understand the basic concepts.

You must use your real name when it asks for a name.

The test will only submit when you have answers all of the questions correctly.

If you are not taking this course for credit please do not answer all the questions correctly for I don't want to be flooded with email answers to the tests.