Nature of Matter

Toward the end of the 19th century, physics thought that only a few details were left to complete regarding their understanding of nature. The head of a physics department told a young man named Planck that he should not go into physics because all of the major problems had been solved. Then the situation began to rapidly change.

help Here is an excellent site describing in much more detail the development of quantum mechanics

1900 Planck did go into physics and he studied the radiation emitted by a solid material heated to incandescence. He found that the present understanding of the physics of such a situation did not correspond to the experimental data. The deviation was in the ultraviolet region of the em spectrum and hence was called the UV catastrophe. Planck was able to make the theory work if he assumed that the body emitted the radiation in a quantized manner rather than in a continuous set of energies. Such an hypothesis was not well received by the smug physics community.

1905 Einstein used the Planck hypothesis and applied it to another problem which had defied solution by classical physics (physics based upon Newton's laws of motion) -- the photoelectric effect. He was able to obtain results agreeing with experiment when he assumed that the waves were quantized and energy was transmitted in packets called quanta and then called "photons". The energy equation is

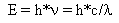
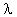Where stands for the Greek letter "nu" and is the frequency. stands for the Greek letter "lambda" which represents the wavelength, and h is Planck's constant.

1910 By this time the physics community had reams of spectra from atoms which showed line spectra rather than continuous spectra. The study of the hydrogen atom spectrum showed very narrow bands with the characteristic wavelengths and colors shown in the table below:

Wavelength	Color
656.2	red
486.1	blue-green
434.0	blue-violet
410.1	violet

These and other lines found in the spectra were found to Four more series of lines were to fit the same general equation given below:

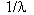= R_H{1/n₁² - 1/n₂²}

where n₁ and n₂ are integers and R_H is 1.09678 x 10^-2 nm^-1called the Rydberg constant which was the most accurately known constant at the time. in the above equation is the wavelength of the light.

help Go to this site for some further examples of continuous and line spectra.

1911 Rutherford suggested a model of the hydrogen atom which had a hydrogen nucleus with an electron orbiting this nucleus. However he used classical physics which says that an orbiting charged particle emits radiation so that it is losing energy and will spiral into the nucleus. This model predicts a very short lifetime for an atom!

1915 Bohr introduced his model of the atom in which he utilized Planck's quantization result -- we will discuss this in the next section.

1923 Using Einstein's equation E = mc² and the above equation for the energy of the photons: 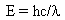and setting them equal gives

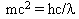
and if we solve for 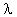we have

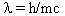
Then de Broglie substituted v for the velocity of a particle to have the amazing result

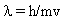
This says that the particle has a wavelength and the previous equation says that light of frequency 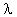has a mass! This result was confirmed experimentally by Davisson in 1927. Now we have the principle of duality -- matter has a wave nature and waves have a matter nature. This was really a remarkable turn of events! We will follow up on this in a later section.

Now take a practice quiz to help you understand if you understand the basic concepts.

You must use your real name when it asks for a name.

The test will only submit when you have answers all of the questions correctly.

If you are not taking this course for credit please do not answer all the questions correctly for I don't want to be flooded with email answers to the tests.