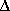 G. If the reaction is at equilibrium
G. If the reaction is at equilibrium 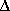 G will be zero for at equilibrium there is no
further net advancement of the reaction. For the reaction
G will be zero for at equilibrium there is no
further net advancement of the reaction. For the reaction
In this section you will learn of an important relationship between the equilibrium constant for a reaction and the change in Gibbs free energy for the reaction.
Synopsis
The reaction free energy is the change in G due to the displacement (or advancement) of the reaction and is given by the symbol 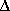 G. If the reaction is at equilibrium
G. If the reaction is at equilibrium 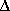 G will be zero for at equilibrium there is no
further net advancement of the reaction. For the reaction
G will be zero for at equilibrium there is no
further net advancement of the reaction. For the reaction
aA + bB 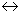 cC + dD
cC + dD
the reaction quotient (Chapter 16) is Q = [C]c[D]d/([A]a[B]b) and the relationship between the reaction free energy, the reaction quotient and the 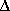 Gosystem is
Gosystem is
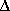 G = [delta]Go + RTlnQ
G = [delta]Go + RTlnQ
At equilibrium, 0 = 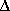 Go + RTlnKc where Kc is the value of the reaction quotient at equilibrium and is the thermodynamic equilibrium constant:
Go + RTlnKc where Kc is the value of the reaction quotient at equilibrium and is the thermodynamic equilibrium constant:
K = [C]c[D]d/([A]a[B]b)equil
We then have that 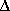 Go = -RTlnKc which is a very useful equation. From this equation we can use values of thermodynamic data to calculate equilibrium constants. If the reactants and products are gases the Q will
be expressed in terms of the partial pressures of the gases rather than the concentrations and the corresponding equilibrium constant would be written as Kp.
Go = -RTlnKc which is a very useful equation. From this equation we can use values of thermodynamic data to calculate equilibrium constants. If the reactants and products are gases the Q will
be expressed in terms of the partial pressures of the gases rather than the concentrations and the corresponding equilibrium constant would be written as Kp.
In section 16.3 we determined that
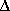 Go = -RTlnKc that if K > 1,
Go = -RTlnKc that if K > 1, 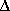 Go will be negative so that the products will be favored at equilibrium. If K is less than 1,
Go will be negative so that the products will be favored at equilibrium. If K is less than 1, 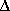 Go will
be positive and the reactants will be favored at equilibrium. These observations are neatly seen in Figure 20.11 in your text.
Go will
be positive and the reactants will be favored at equilibrium. These observations are neatly seen in Figure 20.11 in your text.
Review Question
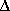 Go and K at 298 (assumed to be at equilibrium). See problem at end of last section for data.
Go and K at 298 (assumed to be at equilibrium). See problem at end of last section for data.

Web Author: Dr. Leon L. Combs
Copyright ©2000 by Dr. Leon L. Combs - ALL RIGHTS RESERVED