Solubility and Common Ions
Learning Goals
You will now learn how to consider the effect on the solubility of a salt by a common ion in solution.
Synopsis
In chapter 18 we studied the effect of a common ion on the pH of a solution. We know that we can deal with the common ion effect by applying the Le Chatelier principle to the situation. With the salt dissociation AaBb 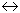 aA+ + bB-, we know that the Le
Chatelier principle tells that an added amount of A+ or B- ions will shift the reaction to the left; that is, it will decrease the solubility of the salt. We can easily calculate the solubility of the salt in the solution containing a common ion. To
simplify the situation, let's assume that we have a 1-1 salt like AgCl and that we want to determine the solubility of the salt when we add the AgCl to a solution which already contains b M concentration of Cl- ions. We can set up a table as we have
done many times before to solve the problem:
aA+ + bB-, we know that the Le
Chatelier principle tells that an added amount of A+ or B- ions will shift the reaction to the left; that is, it will decrease the solubility of the salt. We can easily calculate the solubility of the salt in the solution containing a common ion. To
simplify the situation, let's assume that we have a 1-1 salt like AgCl and that we want to determine the solubility of the salt when we add the AgCl to a solution which already contains b M concentration of Cl- ions. We can set up a table as we have
done many times before to solve the problem:
| cond | Ag+ | Cl- |
| Initial concentration , M | 0 | b |
| Change | x | x |
| At equilibrium | x | x + b |
Now we have that Ksp = x (x + b) = x2 + bx or we have x2 + bx - Ksp = 0.
This would then give us x = ½(-b (+/-)(b2 +4Ksp)1/2)
or if we ignore x in comparison to b, x = Ksp/b. And because this is a 1-1 salt, the value of x is the solubility of the salt. For AgCl, Ksp is 1.8 x 10-10 to if we put solid AgCl into a one liter solution that already has a concentration of
Cl- ions of 0.200 M, the solubility of AgCl would be 9.0 x 10-10 M. The solubility of AgCl in pure water is 1.3 x 10-10 M so there has been a considerable reduction in the solubility of AgCl by the addition of Cl- ions.
You should always check the validity of assuming that x much less than b, but for these solubility problems, it will almost always be an excellent approximation. You can check your assumption by using the value calculated for x into the expression Ksp =
x (x + b), and see if the calculated value of Ksp agrees with its given value.
We don't always have a 1-1 salt, so we have to consider how to calculate the solubility of other types of salts and the change in solubility of such salts due to the presence of a common ion. If the salt is a "1-b" type salt then we could just choose
the concentration of the "1" ions as the solubility of the salt. For example, for AuI3, the concentration of Au3+ ions in solution would be the solubility of the salt. If the salt is a "a-b" type of salt such as Fe2S3, the situation is a little more
complex. The equilibrium would be like our hypothetical AaBb--> aA+ + bB- and we can just choose one of the ions as our reference ion and set up a table as before.
Let's do an example calculation for AuI3. First we calculate the solubility of the salt in pure water.
| conc | Au3+ | I- |
| Initial concentration, M | 0 | 0 |
| Change | +(1/3)x | +x |
| Equilibrium, M | (1/3)x | x |
We would then solve Ksp = (1/3)x(x3) for x; the concentration of I- ions and the solubility of AuI3. Now we would do a similar setup and calculation for the solubility of the salt in solution if one of the product ions began with a certain
concentration.
| conc | Au3+ | I- |
| Initial concentration, M | 0 | b |
| Change | ,+(1/3)x | +x |
| Equilibrium, M | (1/3)x | x + b |
Now we would have Ksp = (1/3)x(x + b)3 and we would have to solve this for x ; again, the concentration of I- ions and the solubility of AuI3 in the presence of additional I-.
Review Questions
- Calculate the solubility of CaF2 in water.
- Calculate the solubility of CaF2 in a water solution that already has F- ions present in the concentration of 2.45 x 10-4 M.

Web Author: Dr. Leon L. Combs
Copyright ©2000 by Dr. Leon L. Combs - ALL RIGHTS RESERVED
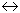 aA+ + bB-, we know that the Le
Chatelier principle tells that an added amount of A+ or B- ions will shift the reaction to the left; that is, it will decrease the solubility of the salt. We can easily calculate the solubility of the salt in the solution containing a common ion. To
simplify the situation, let's assume that we have a 1-1 salt like AgCl and that we want to determine the solubility of the salt when we add the AgCl to a solution which already contains b M concentration of Cl- ions. We can set up a table as we have
done many times before to solve the problem:
aA+ + bB-, we know that the Le
Chatelier principle tells that an added amount of A+ or B- ions will shift the reaction to the left; that is, it will decrease the solubility of the salt. We can easily calculate the solubility of the salt in the solution containing a common ion. To
simplify the situation, let's assume that we have a 1-1 salt like AgCl and that we want to determine the solubility of the salt when we add the AgCl to a solution which already contains b M concentration of Cl- ions. We can set up a table as we have
done many times before to solve the problem:
