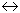Polyprotic Acids and Bases

Learning Goals

You will now learn how to calculate the pH of an aqueous solution of a polyprotic acid or base.

Synopsis

Polyprotic acids and bases present a bit more of a complicated situation because we will have to deal with a multi-step dissociation and a different equilibrium constant for each step. The equilibrium constants become smaller at each step. Sulfuric acid is a diprotic acid so it will have two dissociation steps and we will have two equilibrium constants, one for each step. For sulfuric acid we will have a Ka₁ and a Ka₂ with Ka₁ > Ka₂. Phosphoric acid is a triprotic acid and so will have three dissociation steps. The procedure is the same as before except that we now have more than one step involved.

So let's work a sulfuric acid example. Suppose that we start with 0.100 M H₂SO₄ which is a very strong acid and even the Ka₂ is 1.2 x 10^-2. So we have

H₂SO₄(aq) + H₂O(l) 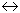H₃O⁺(aq) + HSO₄^-(aq).

Ka1 is very large so we will assume that the 0.100 M H₂SO₄ solution gives us 0.100 M H₃O⁺ and 0.100 M HSO₄^- so that we will have for the second step

HSO₄^-(aq) + H₂O(l) 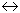H₃O⁺(aq) SO₄^-2(aq)

So let's make up another table:

HSO₄^- H₃O⁺ SO₄^-2

Initial,M 0.100 0.100 0

Change,M -x +x +x

Equilibrium,M 0.100 -x 0.100 + x x

Then for the equilibrium constant we have

K₂ = (0.100 + x) (x)/(0.100 -x) = 1.2 x 10^-2

For this problem we cannot ignore x compared to 0.100 because K is so large. So we set up the quadratic equation

x² + 0.112 x - 0.0012 = 0

and solve for x which gives x = 0.0379. So, we now have the equilibrium value of the hydronium ion concentration (0.1379 M) and the pH is then 0.86 rather than the 1.00 value that it would be if only the first step were considered. The sulfate ion concentration is 0.0379 M, and the HSO₄^- concentration is 0.621 M.

This problem is unusual because we started with a strong acid. The second step is then like a weak acid problem except that the equilibrium constant is still pretty large. For a weak polyprotic acid the situation would be different for now we would have to treat each step like we treated the second step above.

For most weak acids (H₂A), the second equilibrium constant is usually much smaller than the first constant so that we can assume that the hydronium ion concentration overall comes solely from the first step. The [H₃O+] is then equal to {(Ka1)([H₂A]_o}1/2 where [H₂A]_o is the initial concentration of the weak acid. The concentration of the anion, A₂^-, is then just equal to the Ka₂..

Review Questions

What is the pH of a 0.100 M solution of carbonic acid (H₂CO₃)? What is the equilibrium concentration of the carbonate ion?
What is the pH of a 0.100 M solution of phosphoric acid?

	HSO₄^-	H₃O⁺	SO₄^-2
Initial,M	0.100	0.100	0
Change,M	-x	+x	+x
Equilibrium,M	0.100 -x	0.100 + x	x