Calculating Equlibrium Constants
Learning Goals
You will learn two different methods of calculating an equilibrium constant and should be comfortable with both methods before going to the next section.
Synopsis
The first method is quite straight forward. If we know the equilibrium values of all of the reactants and products then we simply substitute the values into the expression for the equilibrium constant and admire the result.
However, life is usually not that simple. Usually we will know the initial concentrations of reactants (because we measured them into the reactant vessel) and the equilibrium concentration of one of the reactants or products after the reaction has
proceeded to equilibrium. We do not want you memorizing a procedure. We want you to reason the solution. Suppose that we have the reaction 2 SO2 + O2 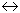 2 SO3 again. Now suppose that you measure a moles of
SO2 and b moles of O2 into the reaction vessel at 1000 K (remember that a and b are known values - you measured them). After equilibrium is established, how much of each compound will be present? Reason the answer. There will be
x moles of O2 gone, 2x moles of SO2 gone, and 2x moles of SO3 formed according to what we learned in Chapter 4. Now that we have done the logic we can set up a table like the following:
2 SO3 again. Now suppose that you measure a moles of
SO2 and b moles of O2 into the reaction vessel at 1000 K (remember that a and b are known values - you measured them). After equilibrium is established, how much of each compound will be present? Reason the answer. There will be
x moles of O2 gone, 2x moles of SO2 gone, and 2x moles of SO3 formed according to what we learned in Chapter 4. Now that we have done the logic we can set up a table like the following:
| Information | SO2 | O2 | SO3 |
| Initial moles | a | b | 0 |
| Change as reacts | -2x | -x | 2x |
| Moles at equilibrium | a - 2x | b - x | 2x |
| Equilibrium concentration | (a - 2x)/vol.(liters) | (b - x)/vol.(liters) | 2x/vol(liters) |
So let's assume that we put 1.00 mol of SO2 and 1.00 mol of O2 into a 1.00-L flask and that after equilibrium is established you have formed 0.925 moles of SO3. What is Kc? We set up the above table in
relationship to the stoichiometric coefficients, but the result is given in terms of moles of SO3 so that means that 2x = 0.925, or x = 0.4625 moles. So the table becomes:
| Information | SO2 | O2 | SO3 |
| Initial moles | 1.00 | 1.00 | 0 |
| Change as reacts | -0.925 | -0.4625 | 0.925 |
| Moles at equilibrium | 1 - 0.925 | 1.00 - 0.4625 | 0.925 |
| Equilibrium concentration | (0.075)/1(liters) | (0.5375/1(liters) | 0.925/1(liters) |
Therefore we have that Kc (1000K) = 0.9252/(0.0752 * 0.5375) = 283. Notice that your text assigned the x value to SO2 and SO3, but we assigned the x value to O2, but we each arrived at the same answer.
Obviously it does not matter as long as you are careful throughout the solving of the problem.
We can work similar problems involving gases by using Kp instead of Kc. The process is exactly the same except that we use partial pressures instead of concentrations.
If the ideal gas law is obeyed, PV = nRT, we can solve for P = RT(n/V) = CRT, where C is the concentration in moles/liter. The partial pressure for each gas is then proportional to the concentration of each gas. We can get a relationship between the
Kc and the Kp by solving for C = P/RT and substituting this for each gas in our general reaction aA + bB --> cC +dD:
Kc = {[C]c[D]d / [A]a[B]b}eq = {PCcPDd/(PAaPBb)}eq RTa+b_c_d =
KpRTa+b-c-d
Because the partial pressure is directly proportional to the number of moles, we can set up a table just like the ones above except we use partial pressures instead of moles.
Review Questions
- Prove the above relationship between Kc and Kp.
- Good site and you can calculate some equilibrium constants.

Web Author: Dr. Leon L. Combs
Copyright ©2000 by Dr. Leon L. Combs - ALL RIGHTS RESERVED
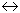 2 SO3 again. Now suppose that you measure a moles of
SO2 and b moles of O2 into the reaction vessel at 1000 K (remember that a and b are known values - you measured them). After equilibrium is established, how much of each compound will be present? Reason the answer. There will be
x moles of O2 gone, 2x moles of SO2 gone, and 2x moles of SO3 formed according to what we learned in Chapter 4. Now that we have done the logic we can set up a table like the following:
2 SO3 again. Now suppose that you measure a moles of
SO2 and b moles of O2 into the reaction vessel at 1000 K (remember that a and b are known values - you measured them). After equilibrium is established, how much of each compound will be present? Reason the answer. There will be
x moles of O2 gone, 2x moles of SO2 gone, and 2x moles of SO3 formed according to what we learned in Chapter 4. Now that we have done the logic we can set up a table like the following:
