Molecular View of Rates

Synopsis

There are two commonly used models used to try to understand chemical reactions on a particulate level. One is called "collision theory" and the other is called the "theory of absolute reaction rates". The second method is more elegant, but also considerably more complicated. The collision theory is basically concerned with the three assumptions:

molecules must collide to react
molecules must collide with sufficient energy to react
molecules must collide in the proper orientation to react

Regarding the first condition, which certainly seems obvious, we know that if we increase the concentration of molecules in the container we will increase the number of collisions, and therefore increase the rate of the reaction. We say then that the rate of the reaction is directly related to the concentrations of the reactants: r = k[A][B].

Regarding the second condition, we can deduce that there is an energy barrier separating the reactants from the products:

Refer to FIGURE 15.13 FROM PAGE 625 HERE.

Unless the energy of the collision supplies enough energy for the reaction to proceed over this barrier, the reaction will not proceed. This energy barrier is called the activation energy, E_a. We have seen in Chapter 12 that the number of molecules with certain energy values has a Boltzmann distribution and the distribution is temperature dependent:

Refer to FIGURE 15.12 FROM PAGE 614 HERE

At higher temperatures there will be a larger percentage of molecules with sufficient energy to overcome the energy barrier and the rate of the reaction will increase. This temperature dependence of the rate constant is given by the Arrhenius equation:

k = A exp(-E_a/RT)

where A is called the frequency factor, which is related to the number of collisions, and R is the gas constant with units of 8.314510 x 10^-3 kJ/(Kmol).

The Arrhenius equation can easily be modified into an equation of a straight line by taking the natural logarithm of each side:

lnk = lnA - E_a/RT

Now if we plot lnk vs. 1/T the intercept will be lnA and the slope will be -E_a/R so we can experimentally obtain the activation energy and the frequency factor (assuming that A and Ea are not functions of temperature) for a reaction. If you only have two sets of data then you can just use them directly because you will have (the lnA's will cancel)

ln(k₂/k₁) = - (E_a/R) (1/T₂ - 1/T₁)

Regarding the third condition, certainly the orientation is essential for reaction to occur unless both reactants are spheres. For large, complicated molecules, only a small fraction of actual collisions will be effectively oriented for reaction to occur. This condition is referred to as the steric condition or the steric factor. Some researchers modify the rate law by inserting the steric factor (sf) into the rate equation

r = (sf) k [A][B]

Much time has been spent on research to try to determine an equation for the steric factor but mainly in context with the theory of absolute reaction rates.

The second model for chemical kinetics is the theory of absolute reaction rates which was developed by Henry Eyring in 1935. It has the basic assumption that the reactions are always in equilibrium with an activated complex (a configuration of atoms involved in the reaction, which is at the top of the energy barrier separating reactants from products) and then this activated complex decomposes into products:

A + B --> [AB]^* --> P

An equation emerges from this theory for the steric factor which makes the model more appealing to people dealing in theories. However the method requires considerably more mathematics and physics than appropriate at this level.

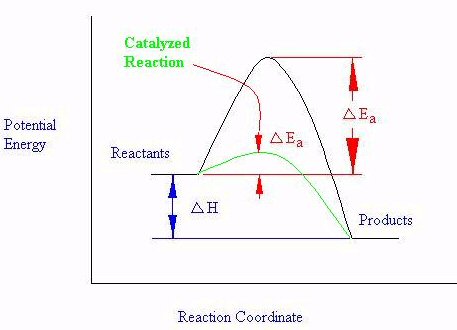
Catalysts are substances that modify the rate of a chemical equation. A positive catalyst will increase the rate and a negative catalyst will decrease the rate. Both kinds of catalysts are useful in industry, but we will concentrate on the positive catalyst effect. A catalyst modifies the rate of a chemical equation by modifying the energy barrier to the reaction proceeding. A positive catalyst will lower the barrier, which allows more collisions to be effective at a particular temperature:

A heterogeneous catalyst is one that is in a different phase than the reactants, such as the potato in the hydrogen peroxide experiment and the catalyst used in the automobile catalytic converter. Most catalysts used in industrial processes are heterogeneous. Your text uses an example of a homogeneous catalyst with iodine serving as a catalyst in the conversion of cis-C₄H₈ to trans-C₄H₈. Neither type of catalyst normally appears in the balanced overall reaction.

Review Questions

Work problem 47 at the end of the chapter.
Work Exercise 15.10 on page 718.
Work problem 41 at the end of the chapter.
Go to this site for further information on catalysis