"Colligative" means bound together by a common origin. The properties to be studied in this section are bound together by a common origin. We can think of the commonality as all of these properties depend not upon what is dissolved but rather how many particles are dissolved. Because of the particle dependency, we will need to use molality rather than molarity. The first property studied here is the change in the vapor pressure, which was first studied by Francois Raoult. It was noted that as a nonvolatile solute was added to a pure volatile solvent, the vapor pressure of the solution decreased as the amount of nonvolatile solute was increased:

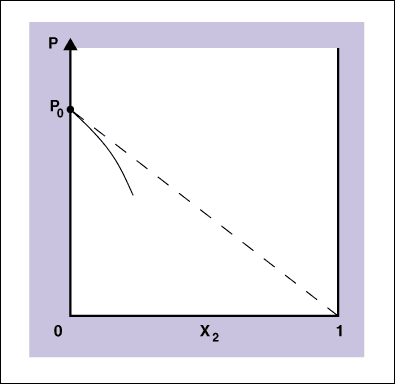
The solid curve is experimental and the dashed curve is ideal. The vapor pressure is P, the vapor pressure of the pure solvent is Po, the mole fraction of the solvent is x, and the mole fraction of the solute is x2. The equation for the dashed line is just the equation for a straight line: P = Po - Pox2. Remember that the equation of a straight line is y = mx + b where b is the x-intercept and m is the slope. In this curve the intercept is Po, and the slope of the line is -Po. If we factor out the Po then we have P= Po(1 - x2), but because there are only two components, x + x2 is equal to one and then 1 - x2 is equal to x so we have P = xPo which is Raoult's law. We see then that Raoult's law is a "limiting law" in the same manner that the ideal gas is a limiting law.
Limiting laws are laws that are valid under some limiting conditions. The ideal gas law is a limiting law in the sense that every real gas will obey the ideal gas law in the limit of zero pressure. From the above diagram you see that Raoult's law is a limiting law in the sense that all solutions will obey Raoult's law in the limit of zero mole fraction of solute. Then for many practical purposes, many solutions will obey Raoult's law at low mole fractions of solute. On a molecular scale we see that the vapor pressure of the solution is lower than the vapor pressure of the pure solvent because of the intermolecular attractions between the solute and the solvent molecules. The intermolecular attractions mean that more energy is needed to get the volatile solvent molecules into the vapor state, and thus at a particular temperature the vapor pressure is lowered by the addition of a nonvolatile solute.
We can calculate the vapor pressure lowering, Po - P, by substituting Raoult's law, P =xPo, for P which gives Po - P = Po - xPo = x2P. We see then that the vapor pressure lowing is directly proportional to the mole fraction of nonvolatile solute. The relative vapor pressure lowering is then (Po - P)/Po = x2, so we can calculate the relative vapor pressure lowering just by calculating the mole fraction of solute in solution.
Now it probably seems obvious that because the vapor pressure of the solvent is lowered by the addition of a nonvolatile solute, the boiling point of the solution will be elevated over the boiling point of the pure solvent. To see this you just have to remember the definition of boiling point: it is the temperature at which the vapor pressure is equal to the atmospheric pressure. Because at a particular temperature the vapor pressure is lowered by the presence of a nonvolatile solute, the temperature has to be increased more than normal for the vapor pressure to reach the value of the atmospheric pressure. We have a simple expression for the boiling point elevation
 tbp = Kbp * msolute
tbp = Kbp * msolute
where Kbp is the molal boiling point elevation constant and msolute is the molality of the solute in solution. Your text has some values for Kbp for a few solvents in units of oC/molal in Table 14.3 on page 661.
We have a similar equation for freezing point depression:
 tfp = Kfp* msolute
tfp = Kfp* msolute
where Kfp is the molal freezing point depression constant, and your text has some values of Kfp for a few solvents also in Table 14.3 on page 661.
We can use either freezing point depression or boiling point elevation to obtain the molecular weight of an unknown compound. If we take x grams of an unknown, dissolve it in y kilograms of a suitable solvent, and obtain the new freezing point or boiling point we can determine the molecular weight of the solute. Molality, m, is the number of moles of solute (weight/MW) per kilogram of solvent so from the freezing point depression expression we have
 t*fp = Kfp(xsolute/MWsolute)/y
t*fp = Kfp(xsolute/MWsolute)/y
or MWsolute = Kfp*x/(y)tfp
We can just change the subscripts in the above to "bp" rather than "fp" and use boiling point elevation data. However, because the freezing point depression is much larger than boiling point elevation, and we want to obtain the most accuracy for the determination of the molecular weight of the unknown, we would rather use the freezing point depression experimental data.
Remember now that these colligative properties depend upon the number of particles dissolved so when an ionic compound is dissolved, there are more separate particles in solution than when a covalent compound dissolves. For example if the ionic dissociation is complete, NaCl produces two ions in solution, BaCl2 produces three ions in solution, etc. However, the dissociation is not quite complete so we will not generally have these nice integers for the number of particles in solution. If we write the freezing point depression equation to take into consideration that the number of particles is larger for the cases of the dissolved solutes dissociating, we can have:
where i is the van't Hoff factor. We can solve for the van't Hoff factor and obtain
i =
where [delta]tfpo is the freezing point depression calculated as though there were one particle per mole of the solute, and )tfp is the experimental freezing point depression. Some values of the van't Hoff factor are given in Table
14.5 on page 581 as a function of concentration for two ionic compounds. You see that as the solution becomes more dilute, the van't Hoff factor approaches the expected integer.
The final colligative property is the osmotic pressure. Osmosis is the movement of solvent molecules through a semipermeable membrane. The spontaneous direction of osmosis is from the region of low solute concentration to the region of high solute
concentration. This could be called the "prune principle" because this phenomenon is often seen as people take a prune and put it in water before eating it. The prone, shriveled as it looks, contains a little bit of water and a relatively high
concentration of sugar behind a semipermeable membrane (the skin of the prune). Considering the prune in the water, we see that osmosis of the water will occur from the region of low solute concentration to the region of high solute concentration. The
osmosis will continue until the prune skin bursts from the increased pressure inside the prune - we try to stop the process before we have a mess. This increased pressure is called osmotic pressure because the cause of the increased pressure is the
osmosis. It is always very important to understand what is the cause and what is the effect in any process. The osmotic pressure (Pi) and the concentration of solute is given by a limiting law as
Pi = cRT
Note the similarity to the limiting gas law, P = nRT/V = cRT. The osmotic pressure generally is rather large - the osmotic pressure of common seawater is about 47 atm - so that we can work in very dilute solutions and still have a considerable osmotic
pressure. Working at lower concentrations means that the limiting law is more closely followed by experiment. Because osmotic pressure is very large, it is often used to determine the molecular weights of unknowns rather than freezing point depression.
Reverse osmosis is used in countries near a body of salt water such as the ocean to remove the salts from the water. The salt water is forced through the semipermeable membrane to remove the salts from the water. Rehydration of patients in hospitals is
done with an isotonic (isoosmotic) solution so that the solution does not cause an abnormal osmosis to occur in the cells.
Review Questions
 t*fp =
t*fp =  t*fp/(Kfpmsolute) =
t*fp/(Kfpmsolute) =  t*fp/
t*fp/ tfpo
tfpo

Web Author: Dr. Leon L. Combs
Copyright ©2000 by Dr. Leon L. Combs - ALL RIGHTS RESERVED