Measurement

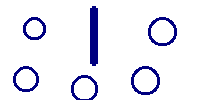
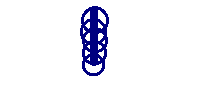
A number with no units is meaningless. If I say that I weigh 90.8 how much information does that convey to you? None, right? However if I put a unit on that and say that I weigh 90.8 kgm, then that is meaningful, although perhaps not a whole lot of help to people who are used to pounds and inches (English system). Another system used by most of the rest of the world is the metric system. However even agreeing to use the metric system is not complete enough.

It is important that everyone throughout the world use the same units of measurement so that we can effectively communicate. Since 1960 scientists have used the SI system of measurement, but not totally as we will see as we progress through the semester. The SI stands for the International System (le Systeme International, in French).

The Fundamental SI Units are as listed below:

Physical Quantity       Name of Unit        Abbreviation
Mass                      kilogram               kg
Length                    meter                   m
Time                      second                  t
Temperature               Kelvin                  K
Electric Current          ampere                  a
Amount of substance       mole                   mol
Luminous intensity        candela                cd

Derived SI units come from combinations of the above such as the following:

area                  square meter                 m2
volume                cubic meter                  m3
velocity              meter per second             m s-1
acceleration          meter per second squared     m s-2
density               kilogram per cubic meter     kg m-3
molar mass            kilogram per mol             kg mol-1
molar volume          cubic meter per mole         m3 mol-1
molar concentration   mole per cubic meter         mol m-3

The prefixes used with these units are given below and in your book (Table 1-2) and you must memorize them today.

Prefix      Symbol     Exponential Notation
exa           E                1018
penta         P                1015
tera          T                1012
giga          G                109
mega          M                106
kilo          k                103
hecto         h                102
deka          da               101
deci          d                10-1
centi         c                10-1
milli         m                10-3
micro         mc or µ          10-6
nano          n                10-9
pico          p                10-12
femto         f                10-15
atto          a                10-18

When you have seen one measurement you have seen them all is certainly not true. There are three concepts involved:

• Accuracy
• Precision
• Measuring Device

If we want to measure this line: ______________________________

we could get several different answers depending upon the measuring device. One device might give 3.5 inches by one person with measuring device A and 3.56 by another person with measuring device B. However when they swap devices, they might not get the same results as recorded initially with A and B. So all three concepts are involved. The slide below neatly shows the difference between accuracy and precision.

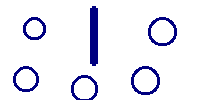
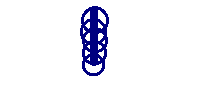
Imagine that the above represents the results of a "ring toss" game. The first image is clearly very precise, but not accurate. The second has rings all over the place and hence is neither precise nor accurate. The third is "just right" -- precisely accurate

Now suppose that person 1 measures the above line with device A and person 2 measures the length of this line __________with device B. What is the sum of the lengths of the two lines? First we must be certain that the accuracy of A is really only in the tenths of inches and the accuracy of B is really to the hundredths of inches. Assuming that such is a fact, then how do we determine the sum? Well now we are into a new topic: significant figures.

There are some rules to follow to allow you to get the significant figures done correctly. I summarize them as follows:

• Non-zero integers always count as significant figures.
• Leading zeros and zeros used to locate the decimal point are not significant. Thus the number 0.002 has only one significant figure.
• Zeros that arise as a part of the measurement are significant. Thus the number 0.005025 has four significant figures.
• What about the number 600? The number of significant figures is ambiguous unless we use scientific notation in which case the number might be represented as 6.00 x 10² if we mean it to have three significant figures, or 6.0 x 10² if the number has only two significant figures.
• Certain values such as those that arise from definitions are exact. For example, there are 1000 ml in one liter and the number 1000 is exact which means that it is not used in determining the final number of significant figures in a product, sum, quotient, or subtraction process. Values obtained by counting are also exact, for example the H₂ molecule contains exactly 2 atoms. A dozen is exactly 12 of something.
• The result of an addition or subtraction should be reported to the same number of decimal places as that of the term with the least number of decimal places.
• The answer to a multiplication or division should be reported to the same number of significant figures as is possessed by the least precise term used in the calculation.
• Rounding is done after all of the calculation is complete. If the figure following the last number to be retained is less than 5, all the unwanted figures are discarded and the last number is left unchanged: 3.7644 is 3.76 to three significant figures. If the number following the last number to be kept is 5 or greater then the last number is rounded up by one: 6.2504 is 6.3 to two significant figures. 6.348 is also 6.3 to two significant figures.

Now you might want to go to This Tutoring Site for more help with significant figures.

Often we have to convert from one system of units to another. For example, you may be wondering how much I really weigh since I told you earlier that I weigh 90.8 kgm. The method of unit conversion is called either the unit factor method or dimensional analysis. In order to make conversions we must know some conversion factors. Two of the more useful are that there are 2.54 cm in one inch and that there are 453.6 gms in one pound. Let's consider the gram/pound conversion.

We have the equality:

453.6 gms = 1 pound

So divide both sides by 453.6 gms and we have

453.6 gms/453.6 gms = 1 = 1 pound/453.6gms

So since 1 pound divided by 453.6gms is equal to one, multiplying by that ratio will not change the value of the numerical value of the number -- just the unit. So let's give it a try.

90.8kgm x 1000gm/kgm = 90800 gms where we used another definition ratio (1000gm/1kgm). Now use the pound conversion:

90800gms x 1 pound/453.6 gms = 200.2 pounds. But what about sig figs? We only have 3 sig figs in the given number of 90.8 kgm so we say that I weigh 200. pounds where I put a "." after the number 200 which indicates that all three digits are significant. Alternatively we could say that I weigh 2.00 x 10² pounds.

Now you might want to go to This Tutoring Site for help in unit conversions.

Now you are ready to go to THIS WEB SITE to practice doing all of the above. In learning this type of material it is crucial to practice.

Now take a practice quiz to help you understand if you understand the basic concepts.

You must use your real name when it asks for a name.

The test will only submit when you have answers all of the questions correctly.

If you are not taking this course for credit please do not answer all the questions correctly for I don't want to be flooded with email answers to the tests.

Web Author: Dr. Leon L. Combs
Copyright ©1999 by Dr. Leon L. Combs - ALL RIGHTS RESERVED