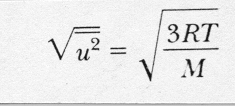Kinetic Molecular Gas Theory

Learning Goals

This section introduces you to a model for understanding the macromolecular properties of this chapter.

Synopsis

This theory is based upon ideal gas behavior with the following assumptions:

Gases consist of molecules whose separation is much greater than the size of the molecules themselves
The molecules of a gas are in continual, random, and rapid motion.
The average kinetic energy of gas molecules is proportional to the gas temperature. This assumption means that all gases have the same average kinetic energy at a particular temperature, regardless of their molecular mass
All collisions are elastic (gas molecules collide with each other and the walls of the container with no transfer or loss of energy)

This model assumes that the sizes of the gas molecules are not important and that there are no intermolecular forces, both of which are assumptions of ideal gas behavior. We can use this model to derive an equation for the root-mean-square (rms) velocity of molecules:

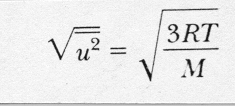mpvelocity ...eq 9

This equation for the rms velocity is also sometimes called "Maxwell's equation" although Maxwell developed many other equations that bear his name (e.g. Maxwell's equations of thermodynamics and Maxwell's equations of electrodynamics) so we should perhaps call it "Maxwell's velocity equation". The following figure shows the Maxwell-Boltzmann velocity distribution of oxygen molecules at different temperatures.

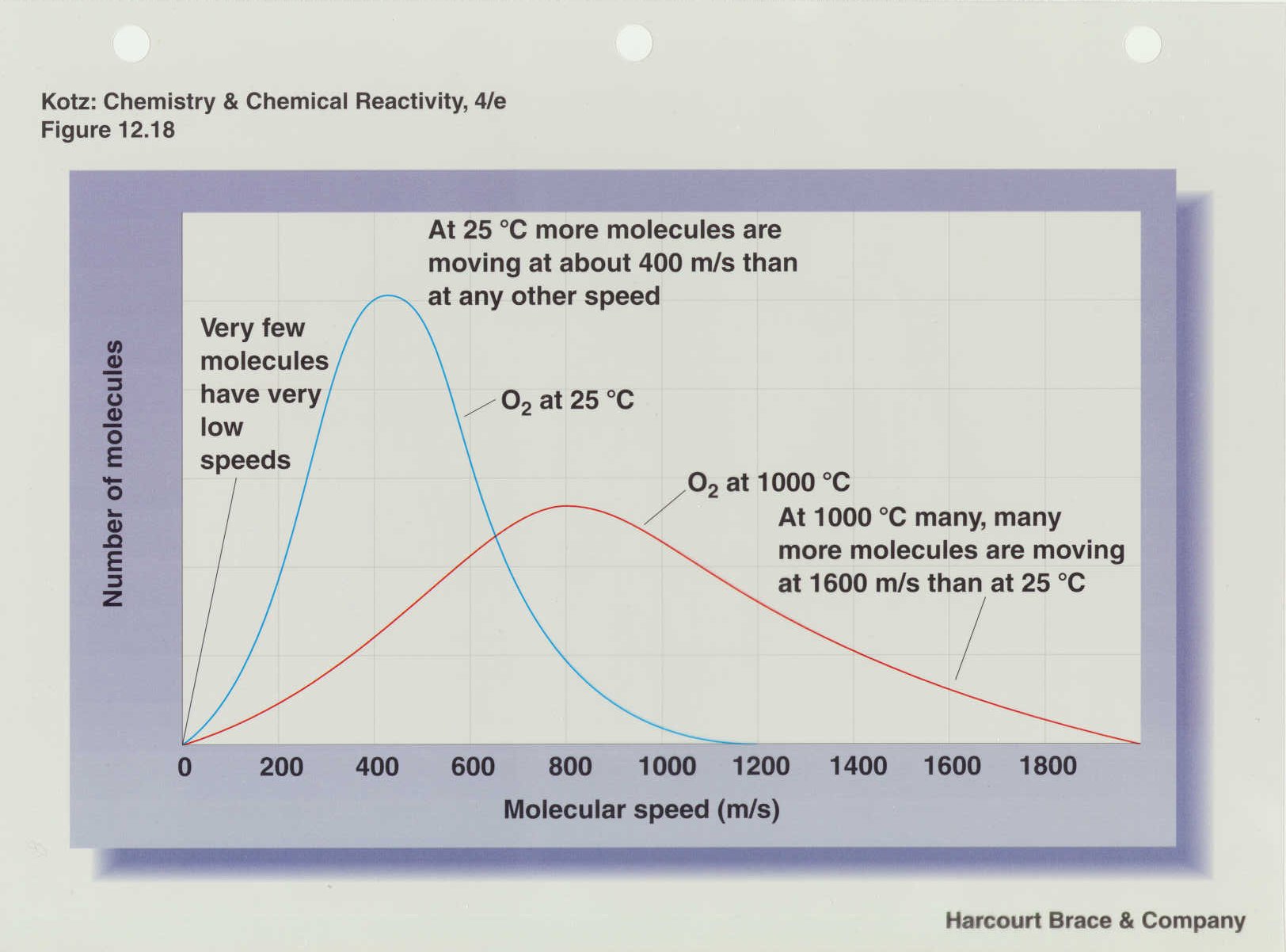
gasdistribution

We can also determine the "most-probable velocity" using this model and that velocity will correlate with the maximum of the distribution (a little over 200 m/s at 25 ^oC and a little over 800 m/s at 1000 ^oC). The equation for this velocity is ump = (2RT/M)^.5. Also note that the curves in the figure above are not symmetrical about the maximum. That means that the average velocity will be another type of velocity and it will be where the areas under the curve on each side of that velocity are equal. The average velocity is given by uav = (8RT/pi*M)^.5. Figure 12.19 in your text shows the Maxwell-Boltzmann velocity distribution for different gases at the same temperature. It is important for you to convert some of these velocities into the more common units in America so that you gain an appreciation for the rate at which events occur on the molecular level.

Review Questions

Calculate the rms velocity, the most-probably velocity, and the average velocity for the oxygen molecule at 25 ^oC. Order your calculated values to verify that ump < uav
Convert the above velocities into "American units" (miles per hour).
What effect will intermolecular forces have on the velocities?
What effect will inelastic collisions have on the velocities?